Research - Natan Andrei\'s research group

Our research develops exact and numerical approaches for quantum many-body systems with an emphasis on
integrability, quantum impurities, boundary phenomena, and open-system dynamics.
We use Bethe ansatz, field theory, and computation to uncover universal features of strongly correlated and non-Hermitian quantum matter.

Current Focus

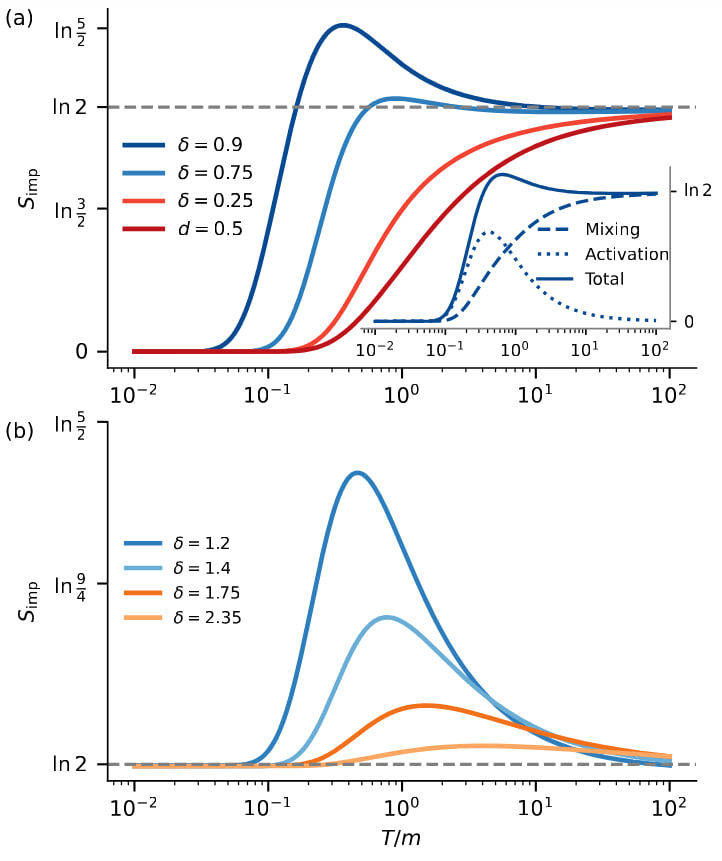
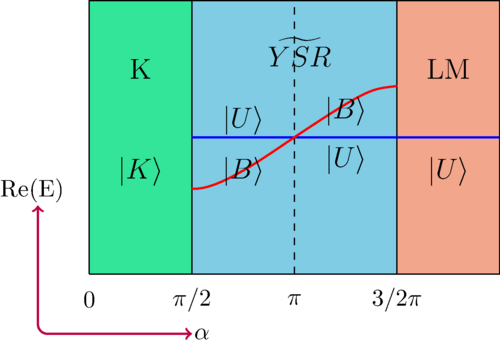
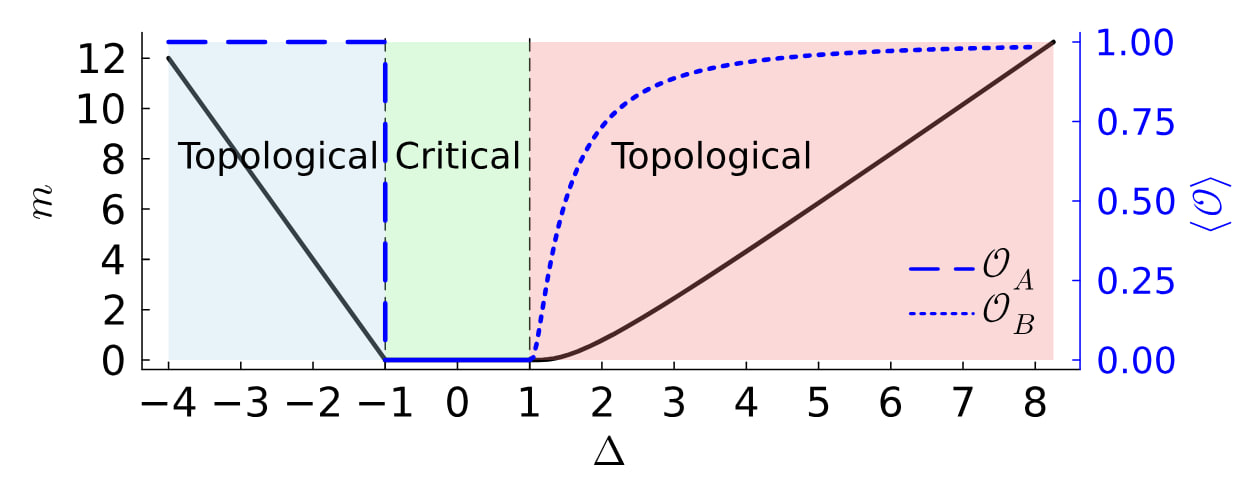
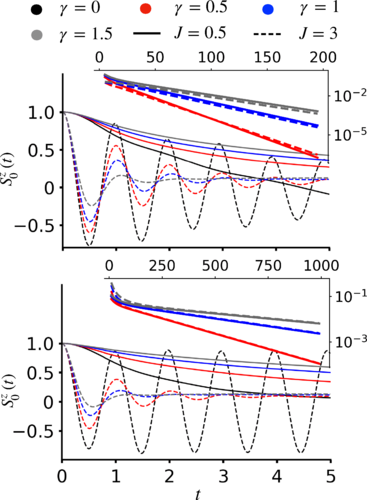
Quantum impurities & boundary-driven phase transitions in 1D.

We investigate impurity-triggered phase transitions in one dimension across lattice and continuum models.
Beyond SU(2) we study XXZ and SU(N) representations and the role of edge magnetic fields, combining Bethe ansatz with numerics to chart boundary criticality and crossover behavior.

Recent papers:

Thermodynamics in a split Hilbert space: Quantum impurity at the edge of a one-dimensional superconductor —
Four impurity phases (Kondo, YSR I/II, local moment) with entropy overshoots arising from split tower structures; closed-form F_imp(T) and impurity entropy across the phase diagram.
Thermodynamics in a split Hilbert space: Quantum impurity at the edge of the Heisenberg chain —
Isotropic S=1/2 chain with an edge impurity showing Kondo, ABM, LM, and FBM phases; analytic origin of entropy undershoots via tower fractionalization, validated against tensor-network/ED.
Competing color superconductivity and color Kondo effect in quark matter —
Exactly solved boundary physics of dense QCD toy models; competition between bulk color pairing and Kondo screening yields a novel single-particle bound-state screening regime.
Kondo overscreening in the presence of superconductivity —
Phase structure with overscreened Kondo, YSR-like midgap screening, and unscreened regimes; a boundary excitation emerges between Kondo and YSR phases.
Spin fractionalization and zero modes in the spin-1/2 XXZ chain with boundary fields —
Fractional edge spin 1/4 as a sharp observable (zero variance) and its connection, at vanishing fields, to a strong zero-energy mode in the low-energy subspace.

Impurities in effective non-Hermitian settings (open/Lindbladian systems).

Open quantum systems governed by Lindbladians can be captured by effective non-Hermitian Hamiltonians. We study impurity physics with gain/loss, exceptional points, and PT symmetry, blending exact solutions with DMRG benchmarks.

Dissipation driven phase transition in the non-Hermitian Kondo model —
RG invariants (generalized T_K, loss strength α) organize Kondo → ~YSR → local-moment phases with a dissipation-driven transition at α=π/2.
Spin chain with non-Hermitian 𝒫𝒯-symmetric boundary couplings: Exact solution, dissipative Kondo effect, and phase transitions on the edge —
Exactly solvable PT-symmetric boundary Kondo model exhibiting PT-unbroken Kondo/LM phases and a bound-mode phase with complex-conjugate eigenpairs; DMRG MPO accuracy benchmarked.

Spontaneous symmetry breaking (SSB) & symmetry-protected topological (SPT) phases.

We analyze how impurities and boundaries interface with ordered and topological phases, constructing dual descriptions and exact boundary operators that diagnose topological order and edge structure.

What is the topological dual of the XXZ spin Chain? —
Non-local map to a local fermionic Hamiltonian exhibiting two SPT phases separated by a Luttinger liquid; string order, entanglement diagnostics, and an exact zero-mode operator.

Open quantum system dynamics.

We study relaxation, transport, and entanglement in driven-dissipative integrable circuits, connecting impurity dynamics, KPZ/balistic to diffusive crossovers, and the quantum Zeno effect.

Quantum Zeno effect in noisy integrable quantum circuits for impurity models —
In XXX/XX chains with dephasing, impurities show bound-mode oscillations vs. Kondo decay; long-time Zeno slowdown tied to bulk crossover from KPZ/ballistic to diffusion under noise.