In many Bayesian inference problems, the geometry of the posterior distribution can vary dramatically in scale. A classic example is Neal’s funnel, where the state-of-the-art algorithm, the No-U-Turn Sampler (NUTS), struggles due to its use of a fixed leapfrog step size.
We’ve just released a new solution: WALNUTS (Within-orbit Adaptive Leapfrog No-U–Turn Sampler), and yes, the acronym did come first. WALNUTS builds on over a decade of progress in locally adaptive Hamiltonian Monte Carlo. It adapts the step size within each orbit—not between orbits, but inside them (see image below). Crucially, it preserves the key features of NUTS: path-length adaptivity and biased progressive sampling.
To do this, WALNUTS introduces a macro/micro timescale:
- Macro steps define the coarse skeleton of the orbit, i.e., the orbit is built by advancing from one macro point to the next.
- Micro steps adapt dynamically between macro points, refining the integration resolution to control local energy error.
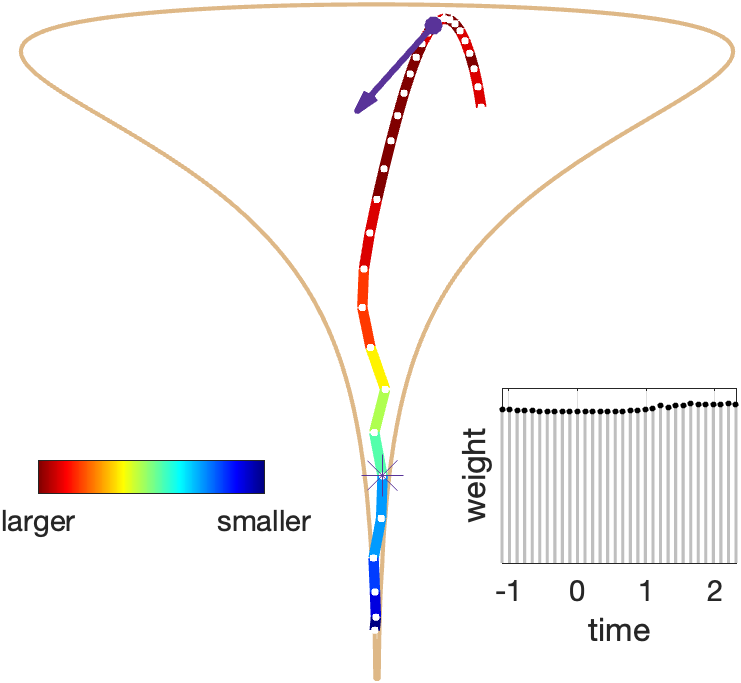
White dots mark macro step positions.
Colored bands represent variable-resolution leapfrog integration.
The star marks the final state, selected via biased progressive sampling using the weights shown in the inset.
The end result is robust, efficient sampling—even deep in the neck of Neal’s funnel. See, e.g., Figure 14 in the preprint below where we drop WALNUTS into one of the most ill-conditioned parts of the target, and yet even from this worst-case initialization, WALNUTS stabilizes, adapts, and escapes – without manual tuning. That’s the strength of within-orbit adaptivity.
🙌 A fun and rewarding collaboration with Bob Carpenter (Flatiron), Tore Selland Kleppe (Norway), and Sifan Liu (Flatiron) — supported by the Flatiron Institute and Rutgers University.
Big thanks to Brian Ward and Steve Bronder for their contributions to a fast and efficient C++ implementation of WALNUTS, and for their help integrating it into the Stan ecosystem.