Research

 

Systems of interest

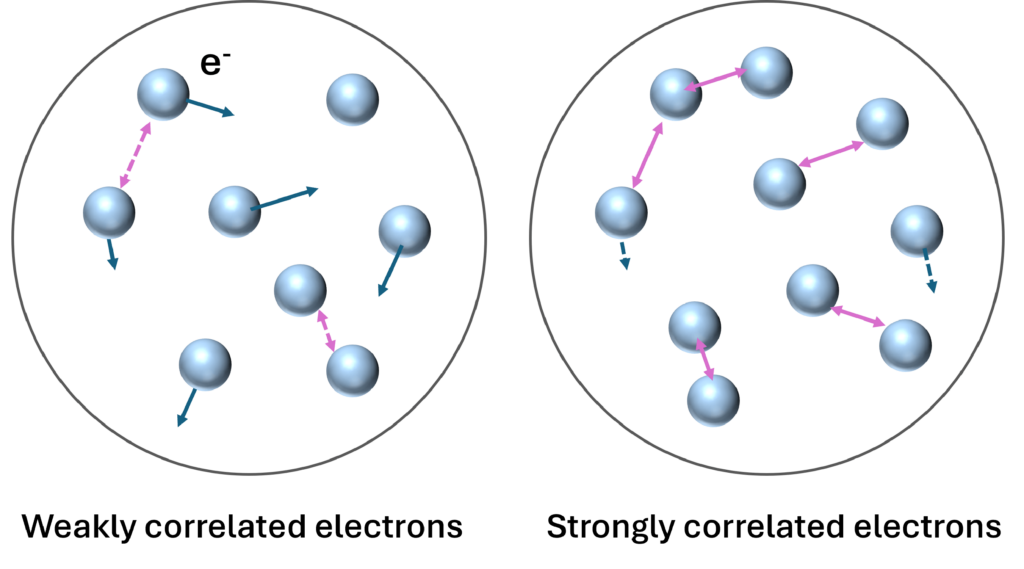Strongly correlated systems represent one of the most challenging problems in chemical simulations. The figure on the left provides a pictorial explanation of weakly and strongly correlated electrons. In strongly correlated systems, electron-electron interactions are significant, making common approximations like the mean-field approximation unreliable. Yet, accurate simulation of these systems is essential, as strong electron correlation underlies many important chemical and physical phenomena, such as catalysis and unconventional superconductivity.

Photovoltaic materials

Photovoltaic (PV) materials are vital to our future clean energy solutions. These materials convert sunlight directly into electricity through the photovoltaic effect. When exposed to light, they absorb photons and generate electron-hole pairs, which are separated to produce an electric current. Our group develops solutions to better understand their properties and design the next generation of PV materials, with particular interest in organic PV and two-dimensional PV systems.

Quantum information materials

Quantum information is a transformative technology with the potential to reshape our future. However, major challenges remain, including limited conceptual understanding and the lack of suitable materials for robust quantum computing. Our mission is to design materials with exotic quantum properties—such as topologically protected orders, fracton phases, and many-body localization—to accelerate progress in quantum information science and technology.

Methods

Quantum embedding methods

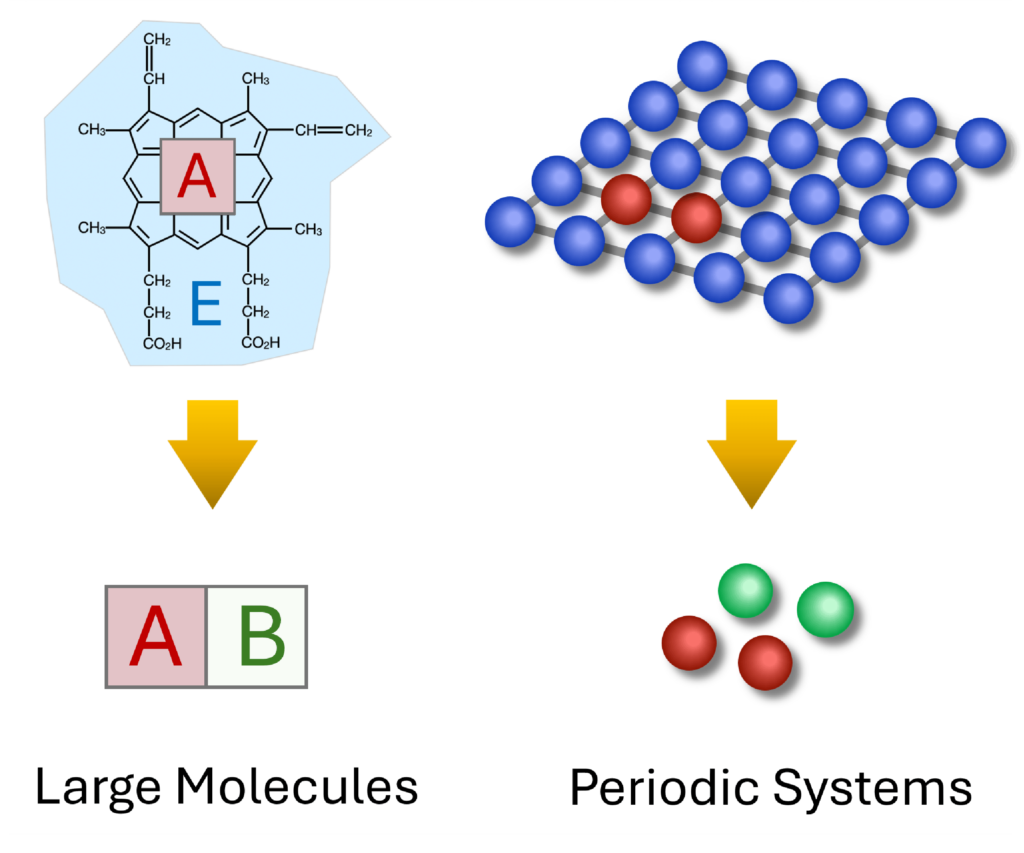Quantum embedding methods are promising tools for scalable chemical simulations. The core idea is to apply different levels of theory to different parts of a system. In materials science, approaches like density matrix embedding theory (DMET, shown in the figure) and dynamical mean-field theory (DMFT) are widely used for their effective treatment of electron correlations. Our group develops embedding methods based on these frameworks to achieve accurate simulations of large solid-state systems.

ML-accelerated quantum chemistry

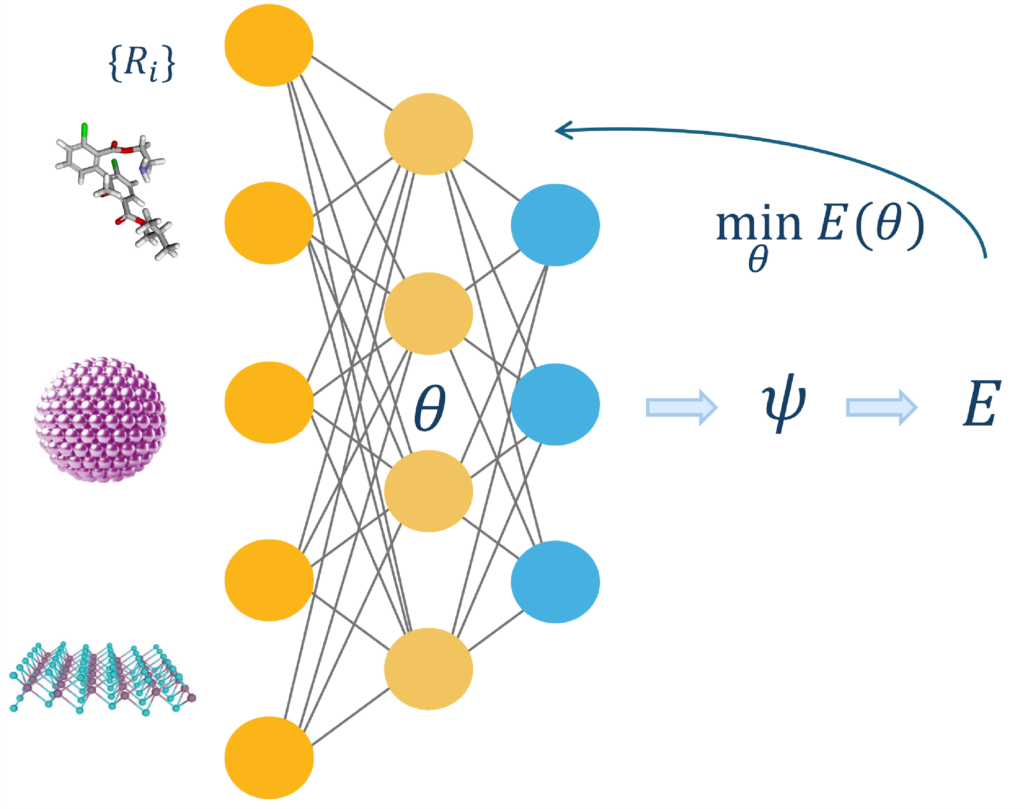Quantum chemistry constantly balances accuracy and computational cost. Machine learning offers two powerful solutions. First, pretrained neural networks can replace the most time-consuming components of quantum chemistry methods, significantly reducing cost while preserving accuracy across diverse systems. Second, the expressiveness of neural networks makes them ideal for representing quantum states—so-called neural network quantum states (NNQS)—which map fundamental system information, such as nuclear coordinates, directly to wavefunctions. Our group advances simulation methods in both directions to accelerate progress in chemical research.

Generative chemical discovery

Chemistry is the science of creating new substances. However, traditional trial-and-error methods are too slow to keep pace with the vastness of chemical space. Recent advances in data science and artificial intelligence offer a path toward systematic and efficient exploration. Our group develops and applies AI tools, guided by quantum chemistry, to accelerate the discovery of novel functional materials.

Publications

Preprints

(2) Cheng, A. H.; Sun, C.; Aspuru-Guzik, A. Scalable Autoregressive 3D Molecule Generation. arXiv, 2025, arXiv:2505.13791.

(1) Sun, C. Electron localization in disordered quantum systems at finite temperatures. arXiv, 2024, arXiv:2403.16868.

Peer-reviewed

(14) Schleich, P.; Calderón, L. M.; Sun, C.; Bagherimehrab, M.; Aldossary, A.; Kottmann, J. S.; Aspuru-Guzik, A. Quantum Computing for Quantum Chemistry; American Chemical Society: Washington, DC, 2025.

(13) Thiede, L.; Sun, C.; Aspuru-Guzik, A. Waveflow: Boundary-conditioned normalizing flows applied to fermionic wave functions. APL Mach. Learn. 2024, 2 (4).

(12) Sun, C.; Gao, F.; Scuseria, G. E. Selected Nonorthogonal Configuration Interaction with Compressed Single and Double Excitations. J. Chem. Theory Comput. 2024, 20 (9), 3741–3748.

(11) Gratsea, K.; Sun, C.; Johnson, P. D. Evaluating the efficiency of ground-state-preparation algorithms. Phys. Rev. A 2024, 109 (4), 042425.

(10) Zhai, H.; Larsson, H. R.; Lee, S.; Cui, Z. H.; Zhu, T.; Sun, C.; Peng, L.; Peng, R.; Liao, K.; Tölle, J.; Yang, J.; Li, S.; Chan, G. K. Block2: A comprehensive open source framework to develop and apply state-of-the-art DMRG algorithms in electronic structure and beyond. J. Chem. Phys. 2023, 159 (23).

(9) Kyaw, T. H.; Soley, M. B.; Allen, B.; Bergold, P.; Sun, C.; Batista, V. S.; Aspuru-Guzik, A. Boosting quantum amplitude exponentially in variational quantum algorithms. Quantum Sci. Technol. 2023, 9 (1), 01LT01.

(8) Ren, F.; Ding, X.; Zheng, M.; Korzinkin, M.; Cai, X.; Zhu, W.; Mantsyzov, A.; Aliper, A.; Aladinskiy, V.; Cao, Z.; Kong, S.; Long, X.; Liu, B. H. M.; Liu, Y.; Naumov, V.; Shneyderman, A.; Ozerov, I. V.; Wang, J.; Pun, F. W.; Polykovskiy, D. A.; Sun, C.; Levitt, M.; Aspuru-Guzik, A.; Zhavoronkov, A. AlphaFold accelerates artificial intelligence powered drug discovery: Efficient discovery of a novel CDK20 small molecule inhibitor. Chem. Sci. 2023, 14 (6), 1443–1452.

(7) Krenn, M.; Ai, Q.; Barthel, S.; Carson, N.; Frei, A.; Frey, N. C.; Friederich, P.; Gaudin, T.; Gayle, A. A.; Jablonka, K. M.; Lameiro, R. F.; Lemm, D.; Lo, A.; Moosavi, S. M.; Nápoles-Duarte, J. M.; Nigam, A. K.; Pollice, R.; Rajan, K.; Schatzschneider, U.; Schwaller, P.; Skreta, M.; Smit, B.; Strieth-Kalthoff, F.; Sun, C.; Tom, G.; von Rudorff, G. F.; Wang, A.; White, A. D.; Young, A.; Yu, R.; Aspuru-Guzik, A. SELFIES and the future of molecular string representations. Patterns 2022, 3 (10).

(6) Sun, C. Finite Temperature Simulations of Strongly Correlated Systems; California Institute of Technology: Pasadena, CA, 2021.

(5) Cui, Z. H.; Sun, C.; Ray, U.; Zheng, B. X.; Sun, Q.; Chan, G. K. L. Ground-state phase diagram of the three-band Hubbard model from density matrix embedding theory. Phys. Rev. Res. 2020, 2 (4), 043259.

(4) Sun, Q.; Zhang, X.; Banerjee, S.; Bao, P.; Barbry, M.; Blunt, N. S.; Bogdanov, N. A.; Booth, G. H.; Chen, J.; Cui, Z.-H.; Eriksen, J. J.; Gao, Y.; Guo, S.; Hermann, J.; Hermes, M. R.; Koh, K.; Koval, P.; Lehtola, S.; Li, Z.; Liu, J.; Mardirossian, N.; McClain, J. D.; Motta, M.; Mussard, B.; Pham, H. Q.; Pulkin, A.; Purwanto, W.; Robinson, P. J.; Ronca, E.; Sayfutyarova, E. R.; Scheurer, M.; Schurkus, H. F.; Smith, J. E. T.; Sun, C.; Sun, S.-N.; Upadhyay, S.; Wagner, L. K.; Wang, X.; White, A.; Whitfield, J. D.; Williamson, M. J.; Wouters, S.; Yang, J.; Yu, J. M.; Zhu, T.; Berkelbach, T. C.; Sharma, S.; Sokolov, A. Y.; Chan, G. K. Recent developments in the PySCF program package. J. Chem. Phys. 2020, 153 (2).

(3) Sun, C.; Ray, U.; Cui, Z. H.; Stoudenmire, M.; Ferrero, M.; Chan, G. K. L. Finite-temperature density matrix embedding theory. Phys. Rev. B 2020, 101 (7), 075131.

(2) Motta, M.; Sun, C.; Tan, A. T. K.; O’Rourke, M. J.; Ye, E.; Minnich, A. J.; Brandao, F. G. S. L.; Chan, G. K.-L. Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. Nat. Phys. 2020, 16 (2), 205–210.

(1) Ye, H. Z.; Sun, C.; Jiang, H. Monte-Carlo simulations of spin-crossover phenomena based on a vibronic Ising-like model with realistic parameters. Phys. Chem. Chem. Phys. 2015, 17 (10), 6801–6808.