Research
In the SI Lab we conduct research around three major thrusts
Data-Driven Modeling of Behavior
Understanding the underlying feedback algorithms of how animals move and learn
Network Inference & Learning
Engineering distributed inference strategies for network systems.
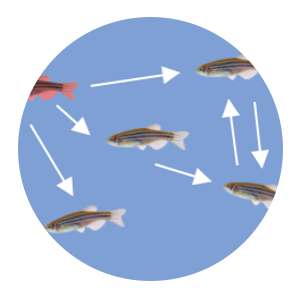
Data-Driven Modeling of Behavior
We are interested in understanding the underlying feedback processes of how animals navigate and orient in complex environments, how they learn, and how they optimally use energy resources. Uncovering these mechanisms can clarify how animals interact with their environment and conspecifics and provide insight into the development of algorithms for inference and control in complex systems.
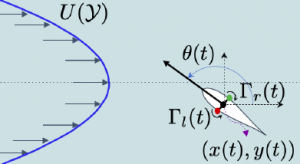
How does a fish swim against the flow? Multisensory feedback control model to explain rheotaxis behavior
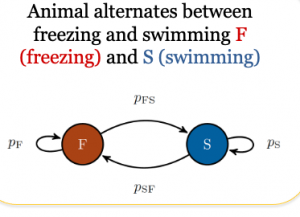
Mathematical model of fish behavior capturing freezing, which is an anxiety-related state
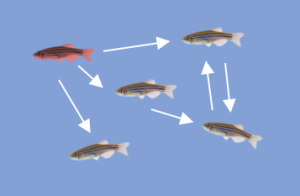
Can positive emotions propagate in a group? We answer this question by studying emotional contagion in zebrafish
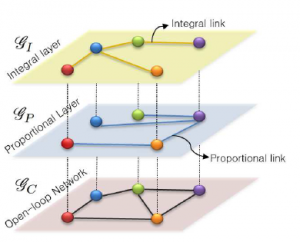
Network Inference & Learning
When designing control strategies for complex systems, a typical assumption is that the dynamics and/or the network topology are known a priori. In real applications, however, such as teams of cooperative robots or biological systems, the network topology, coupling weights, and agent dynamics are time-varying and/or unknown. We are interested in (1) developing strategies to discover the underlying dynamics of complex systems from experimental data and (2) developing strategies to deploy distributed learning strategies in network systems.
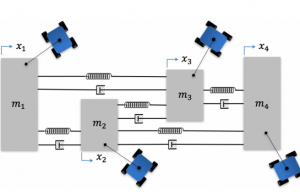
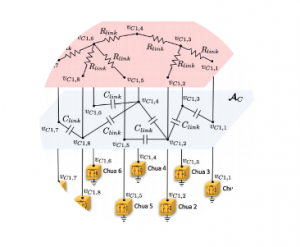
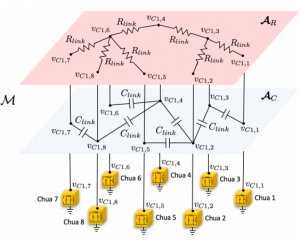
Team of mobile robots using a distributed strategy to estimate an unknown flexible load (a mechanical network of masses interconnected by springs and dampers)
Network Control & Optimization
Our interest is in developing control strategies for complex systems and advancing the mathematical foundations of network control and optimization. The challenge relies on the fact that (1) the number of units is typically large, (2) multiple uncertainties and noise are present across the network, and (3) control interventions can only be applied to a small fraction of the units. The goal is to devise scalable solutions that drive a network into the desired state despite the presence of noise, uncertainties, and limited information. This problem has several applications in engineered and biological systems, such as power grids, robotics, and animal collective behavior